Cas particuliers de résolution de l'équation sinusoïdale. Équations trigonométriques - formules, solutions, exemples. Factorisation

Les principales méthodes de résolution d'équations trigonométriques sont : la réduction des équations au plus simple (à l'aide de formules trigonométriques), l'introduction de nouvelles variables et la factorisation. Regardons leur utilisation avec des exemples. Faites attention au format d'écriture des solutions aux équations trigonométriques.

Une condition nécessaire pour réussir à résoudre des équations trigonométriques est la connaissance des formules trigonométriques (thème 13 du travail 6).

Exemples.

1. Équations réduites au plus simple.

1) Résoudre l'équation

Solution:

Répondre:

2) Trouver les racines de l'équation

(sinx + cosx) 2 = 1 – sinxcosx, appartenant au segment.

Solution:

Répondre:

2. Équations qui se réduisent au quadratique.

1) Résolvez l’équation 2 sin 2 x – cosx –1 = 0.

Solution: En utilisant la formule sin 2 x = 1 – cos 2 x, on obtient

Répondre:

2) Résolvez l'équation cos 2x = 1 + 4 cosx.

Solution: En utilisant la formule cos 2x = 2 cos 2 x – 1, on obtient

Répondre:

3) Résolvez l'équation tgx – 2ctgx + 1 = 0

Solution:

Répondre:

3. Équations homogènes

1) Résolvez l’équation 2sinx – 3cosx = 0

Solution : Soit cosx = 0, puis 2sinx = 0 et sinx = 0 – une contradiction avec le fait que sin 2 x + cos 2 x = 1. Cela signifie cosx ≠ 0 et nous pouvons diviser l'équation par cosx. On a

Répondre:

2) Résolvez l'équation 1 + 7 cos 2 x = 3 sin 2x

Solution:

On utilise les formules 1 = sin 2 x + cos 2 x et sin 2x = 2 sinxcosx, on obtient

péché 2 x + cos 2 x + 7cos 2 x = 6 péchéxcosx
péché 2 x – 6sinxcosx+ 8cos 2 x = 0

Soit cosx = 0, alors sin 2 x = 0 et sinx = 0 – une contradiction avec le fait que sin 2 x + cos 2 x = 1.
Cela signifie cosx ≠ 0 et on peut diviser l'équation par cos 2 x . On a

tg 2 x – 6 tgx + 8 = 0
Notons tgx = y
oui 2 – 6 oui + 8 = 0
oui 1 = 4 ; y2 = 2
a) tgx = 4, x= arctan4 + 2 k, k
b) tgx = 2, x= arctan2 + 2 k, k .

Répondre: arctg4 + 2 k, arctan2 + 2 ok, ok

4. Équations de la forme un péché + b cosx = s, s≠ 0.

1) Résolvez l’équation.

Solution:

Répondre:

5. Équations résolues par factorisation.

1) Résolvez l’équation sin2x – sinx = 0.

Racine de l'équation F (X) = φ ( X) ne peut servir que de nombre 0. Vérifions ceci :

cos 0 = 0 + 1 – l'égalité est vraie.

Le nombre 0 est la seule racine de cette équation.

Répondre: 0.

Vous pouvez commander une solution détaillée à votre problème !!!

Une égalité contenant une inconnue sous le signe d'une fonction trigonométrique (« sin x, cos x, tan x » ou « ctg x ») est appelée une équation trigonométrique, et ce sont leurs formules que nous considérerons plus loin.

Les équations les plus simples sont « sin x=a, cos x=a, tg x=a, ctg x=a », où « x » est l'angle à trouver, « a » est n'importe quel nombre. Écrivons les formules racines de chacun d'eux.

1. Équation `sin x=a`.

Pour `|a|>1`, il n'a pas de solutions.

Quand `|a| \leq 1` a un nombre infini de solutions.

Formule racine : `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Équation `cos x=a`

Pour `|a|>1` - comme dans le cas du sinus, il n'y a pas de solutions parmi les nombres réels.

Quand `|a| \leq 1` a un nombre infini de solutions.

Formule racine : `x=\pm arccos a + 2\pi n, n \in Z`

Cas particuliers du sinus et du cosinus dans les graphiques.

3. Équation `tg x=a`

Possède un nombre infini de solutions pour toutes les valeurs de « a ».

Formule racine : `x=arctg a + \pi n, n \in Z`

4. Équation `ctg x=a`

Possède également un nombre infini de solutions pour toutes les valeurs de « a ».

Formule racine : `x=arcctg a + \pi n, n \in Z`

Formules pour les racines des équations trigonométriques dans le tableau

Pour le sinus :
Pour le cosinus :
Pour la tangente et la cotangente :
Formules pour résoudre des équations contenant des fonctions trigonométriques inverses :

Méthodes de résolution d'équations trigonométriques

La résolution de toute équation trigonométrique comprend deux étapes :

avec l'aide de le transformer au plus simple ;
résolvez l'équation la plus simple obtenue en utilisant les formules de racine et les tableaux écrits ci-dessus.

Examinons les principales méthodes de solution à l'aide d'exemples.

Méthode algébrique.

Cette méthode consiste à remplacer une variable et à la substituer par une égalité.

Exemple. Résolvez l'équation : `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

faites un remplacement : `cos(x+\frac \pi 6)=y`, puis `2y^2-3y+1=0`,

on retrouve les racines : `y_1=1, y_2=1/2`, d'où découlent deux cas :

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Réponse : `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Factorisation.

Exemple. Résolvez l'équation : `sin x+cos x=1`.

Solution. Déplaçons tous les termes de l'égalité vers la gauche : `sin x+cos x-1=0`. En utilisant , nous transformons et factorisons le membre de gauche :

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

`sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
`cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Réponse : `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Réduction à une équation homogène

Tout d’abord, vous devez réduire cette équation trigonométrique à l’une des deux formes suivantes :

`a sin x+b cos x=0` (équation homogène du premier degré) ou `a sin^2 x + b sin x cos x +c cos^2 x=0` (équation homogène du deuxième degré).

Divisez ensuite les deux parties par `cos x \ne 0` - pour le premier cas, et par `cos^2 x \ne 0` - pour le second. Nous obtenons des équations pour `tg x` : `a tg x+b=0` et `a tg^2 x + b tg x +c =0`, qui doivent être résolues à l'aide de méthodes connues.

Exemple. Résolvez l'équation : `2 sin^2 x+sin x cos x - cos^2 x=1`.

Solution. Écrivons le côté droit comme `1=sin^2 x+cos^2 x` :

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Il s'agit d'une équation trigonométrique homogène du deuxième degré, on divise ses côtés gauche et droit par `cos^2 x \ne 0`, on obtient :

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2x+tgx — 2=0`. Introduisons le remplacement `tg x=t`, résultant en `t^2 + t - 2=0`. Les racines de cette équation sont « t_1=-2 » et « t_2=1 ». Alors:

`tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
`tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, `n \in Z`.

Répondre. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

Passer au demi-angle

Exemple. Résolvez l'équation : « 11 sin x - 2 cos x = 10 ».

Solution. Appliquons les formules du double angle, ce qui donne : `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

En appliquant la méthode algébrique décrite ci-dessus, on obtient :

`tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
`tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Répondre. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Introduction de l'angle auxiliaire

Dans l'équation trigonométrique « a sin x + b cos x = c », où a,b,c sont des coefficients et x est une variable, divisez les deux côtés par « sqrt (a^2+b^2) » :

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))`.

Les coefficients du côté gauche ont les propriétés du sinus et du cosinus, à savoir que la somme de leurs carrés est égale à 1 et que leurs modules ne sont pas supérieurs à 1. Notons-les ainsi : `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, alors :

`cos \varphi sin x + sin \varphi cos x =C`.

Regardons de plus près l'exemple suivant :

Exemple. Résolvez l'équation : `3 sin x+4 cos x=2`.

Solution. Divisez les deux côtés de l'égalité par `sqrt (3^2+4^2)`, nous obtenons :

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`

`3/5 péché x+4/5 cos x=2/5`.

Notons `3/5 = cos \varphi` , `4/5=sin \varphi`. Puisque `sin \varphi>0`, `cos \varphi>0`, alors nous prenons `\varphi=arcsin 4/5` comme angle auxiliaire. Ensuite nous écrivons notre égalité sous la forme :

`cos \varphi sin x+sin \varphi cos x=2/5`

En appliquant la formule de la somme des angles pour le sinus, on écrit notre égalité sous la forme suivante :

`sin (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Répondre. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Équations trigonométriques rationnelles fractionnaires

Ce sont des égalités avec des fractions dont les numérateurs et dénominateurs contiennent des fonctions trigonométriques.

Exemple. Résous l'équation. `\frac (sin x)(1+cos x)=1-cos x`.

Solution. Multipliez et divisez le côté droit de l'égalité par « (1+cos x) ». En conséquence nous obtenons :

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

Considérant que le dénominateur ne peut pas être égal à zéro, on obtient `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Assumons le numérateur de la fraction à zéro : `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Alors `sin x=0` ou `1-sin x=0`.

`sin x=0`, `x=\pi n`, `n \in Z`
`1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Étant donné que ` x \ne \pi+2\pi n, n \in Z`, les solutions sont `x=2\pi n, n \in Z` et `x=\pi /2+2\pi n` , `n \in Z`.

Répondre. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

La trigonométrie, et les équations trigonométriques en particulier, sont utilisées dans presque tous les domaines de la géométrie, de la physique et de l'ingénierie. Les études commencent en 10e année, il y a toujours des tâches pour l'examen d'État unifié, alors essayez de vous souvenir de toutes les formules des équations trigonométriques - elles vous seront certainement utiles !

Cependant, vous n'avez même pas besoin de les mémoriser, l'essentiel est d'en comprendre l'essence et de pouvoir la dériver. Ce n'est pas aussi difficile qu'il y paraît. Voyez par vous-même en regardant la vidéo.

Le cours vidéo « Obtenez un A » comprend tous les sujets nécessaires pour réussir l'examen d'État unifié en mathématiques avec 60 à 65 points. Compléter toutes les tâches 1 à 13 de l'examen d'État unifié de profil en mathématiques. Convient également pour réussir l'examen d'État unifié de base en mathématiques. Si vous souhaitez réussir l'examen d'État unifié avec 90 à 100 points, vous devez résoudre la partie 1 en 30 minutes et sans erreurs !

Cours de préparation à l'examen d'État unifié pour les classes 10-11, ainsi que pour les enseignants. Tout ce dont vous avez besoin pour résoudre la partie 1 de l'examen d'État unifié en mathématiques (les 12 premiers problèmes) et le problème 13 (trigonométrie). Et cela représente plus de 70 points à l'examen d'État unifié, et ni un étudiant de 100 points ni un étudiant en sciences humaines ne peuvent s'en passer.

Toute la théorie nécessaire. Solutions rapides, pièges et secrets de l'examen d'État unifié. Toutes les tâches actuelles de la partie 1 de la banque de tâches FIPI ont été analysées. Le cours est entièrement conforme aux exigences de l'examen d'État unifié 2018.

Le cours contient 5 grands sujets de 2,5 heures chacun. Chaque sujet est donné de toutes pièces, simplement et clairement.

Des centaines de tâches d'examen d'État unifié. Problèmes de mots et théorie des probabilités. Algorithmes simples et faciles à retenir pour résoudre des problèmes. Géométrie. Théorie, matériel de référence, analyse de tous types de tâches d'examen d'État unifié. Stéréométrie. Solutions délicates, aide-mémoire utiles, développement de l'imagination spatiale. Trigonométrie de zéro au problème 13. Comprendre au lieu de bachoter. Explications claires de concepts complexes. Algèbre. Racines, puissances et logarithmes, fonction et dérivée. Une base pour résoudre les problèmes complexes de la partie 2 de l'examen d'État unifié.

Les équations trigonométriques les plus simples sont généralement résolues à l'aide de formules. Permettez-moi de vous rappeler que les équations trigonométriques les plus simples sont :

sinx = un

cosx = un

tgx = un

ctgx = un

x est l'angle à trouver,
a est n’importe quel nombre.

Et voici les formules avec lesquelles vous pouvez immédiatement écrire les solutions de ces équations les plus simples.

Pour le sinus :

Pour le cosinus :

x = ± arccos a + 2π n, n ∈ Z

Pour la tangente :

x = arctan a + π n, n ∈ Z

Pour la cotangente :

x = arcctg a + π n, n ∈ Z

En fait, c'est la partie théorique de la résolution des équations trigonométriques les plus simples. D'ailleurs, tout !) Rien du tout. Cependant, le nombre d’erreurs sur ce sujet est tout simplement hors du commun. Surtout si l'exemple s'écarte légèrement du modèle. Pourquoi?

Oui, parce que beaucoup de gens écrivent ces lettres, sans en comprendre du tout le sens ! Il écrit avec prudence, de peur que quelque chose n'arrive...) Il faut régler ce problème. Trigonométrie pour les gens, ou gens pour la trigonométrie, après tout !?)

Voyons ça ?

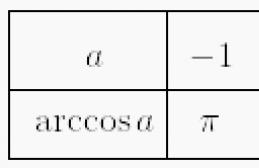
Un angle sera égal à arccos un, deuxième: -arccos a.

Et cela fonctionnera toujours ainsi. Pour toute UN.

Si vous ne me croyez pas, passez votre souris sur l'image ou touchez l'image sur votre tablette.) J'ai changé le numéro UN à quelque chose de négatif. Quoi qu'il en soit, nous avons un coin arccos un, deuxième: -arccos a.

Par conséquent, la réponse peut toujours s’écrire sous la forme de deux séries de racines :

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Combinons ces deux séries en une seule :

x= ± arccos a + 2π n, n ∈ Z

Et c'est tout. Nous avons obtenu une formule générale pour résoudre l'équation trigonométrique la plus simple avec cosinus.

Si vous comprenez qu'il ne s'agit pas d'une sorte de sagesse superscientifique, mais juste une version abrégée de deux séries de réponses, Vous serez également capable de gérer les tâches « C ». Avec des inégalités, avec une sélection de racines dans un intervalle donné... Là, la réponse avec un plus/moins ne fonctionne pas. Mais si vous traitez la réponse de manière pragmatique et la divisez en deux réponses distinctes, tout sera résolu.) En fait, c’est pourquoi nous l’examinons. Quoi, comment et où.

Dans l'équation trigonométrique la plus simple

sinx = un

on obtient également deux séries de racines. Toujours. Et ces deux séries peuvent aussi être enregistrées en une seule ligne. Seule cette ligne sera plus délicate :

x = (-1) n arcsin a + π n, n ∈ Z

Mais l’essence reste la même. Les mathématiciens ont simplement conçu une formule pour créer une entrée au lieu de deux pour une série de racines. C'est tout!

Vérifions les mathématiciens ? Et on ne sait jamais...)

Dans la leçon précédente, la solution (sans aucune formule) d'une équation trigonométrique avec sinus a été discutée en détail :

La réponse a abouti à deux séries de racines :

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Si nous résolvons la même équation en utilisant la formule, nous obtenons la réponse :

x = (-1) n arcsin 0,5 + π n, n ∈ Z

En fait, c'est une réponse inachevée.) L'étudiant doit savoir que arcsin 0,5 = π /6. La réponse complète serait :

x = (-1)n π /6+ π n, n ∈ Z

Cela soulève une question intéressante. Répondre via x1 ; x2 (c'est la bonne réponse !) et par la solitude X (et c'est la bonne réponse !) - est-ce la même chose ou pas ? Nous le découvrirons maintenant.)

Nous remplaçons la réponse par x1 valeurs n =0; 1; 2 ; etc., on compte, on obtient une série de racines :

x 1 = π/6 ; 13π/6 ; 25π/6 et ainsi de suite.

Avec la même substitution en réponse avec x2 , on a:

x2 = 5π/6 ; 17π/6 ; 29π/6 et ainsi de suite.

Maintenant, remplaçons les valeurs n (0 ; 1 ; 2 ; 3 ; 4...) dans la formule générale pour un seul X . C'est-à-dire que nous élevons moins un à la puissance zéro, puis à la première, à la seconde, etc. Eh bien, bien sûr, nous remplaçons 0 dans le deuxième terme ; 1; 2 3 ; 4, etc Et nous comptons. On obtient la série :

X = π/6 ; 5π/6 ; 13π/6 ; 17π/6 ; 25π/6 et ainsi de suite.

C'est tout ce que vous pouvez voir.) La formule générale nous donne exactement les mêmes résultats tout comme les deux réponses séparément. Juste tout à la fois, dans l'ordre. Les mathématiciens n'étaient pas dupes.)

Les formules de résolution d'équations trigonométriques avec tangente et cotangente peuvent également être vérifiées. Mais nous ne le ferons pas.) Ils sont déjà simples.

J'ai écrit spécifiquement toutes ces substitutions et vérifications. Ici, il est important de comprendre une chose simple : il existe des formules pour résoudre des équations trigonométriques élémentaires, juste un bref résumé des réponses. Pour cette brièveté, nous avons dû insérer plus/moins dans la solution cosinus et (-1) n dans la solution sinus.

Ces inserts ne gênent en rien les tâches où il suffit d'écrire la réponse à une équation élémentaire. Mais si vous avez besoin de résoudre une inégalité, ou si vous devez faire quelque chose avec la réponse : sélectionner des racines sur un intervalle, vérifier l'ODZ, etc., ces insertions peuvent facilement déstabiliser une personne.

Donc qu'est ce que je devrais faire? Oui, soit écrivez la réponse en deux séries, soit résolvez l'équation/inégalité à l'aide du cercle trigonométrique. Ensuite ces insertions disparaissent et la vie devient plus facile.)

Nous pouvons résumer.

Pour résoudre les équations trigonométriques les plus simples, il existe des formules de réponse toutes faites. Quatre pièces. Ils sont parfaits pour écrire instantanément la solution d’une équation. Par exemple, vous devez résoudre les équations :

sinx = 0,3

Facilement: x = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Aucun problème: x = ± arccos 0,2 + 2π n, n ∈ Z

tgx = 1,2

Facilement: x = arctan 1,2 + π n, n ∈ Z

ctgx = 3,7

Un dernier: x= arcctg3,7 + π n, n ∈ Z

cosx = 1,8

Si vous, brillant de connaissances, écrivez instantanément la réponse :

x= ± arccos 1,8 + 2π n, n ∈ Z

alors tu brilles déjà, ceci... cela... d'une flaque d'eau.) Bonne réponse : il n'y a pas de solutions. Vous ne comprenez pas pourquoi ? Lisez ce qu'est l'arc cosinus. De plus, si sur le côté droit de l'équation d'origine se trouvent les valeurs tabulaires du sinus, du cosinus, de la tangente, de la cotangente, - 1; 0; √3; 1/2; √3/2 et ainsi de suite. - la réponse à travers les arches sera inachevée. Les arches doivent être converties en radians.

Et si vous rencontrez des inégalités, comme

alors la réponse est :

x πn, n ∈ Z

il y a de rares absurdités, oui...) Ici, vous devez résoudre en utilisant le cercle trigonométrique. Ce que nous ferons dans le sujet correspondant.

Pour ceux qui lisent héroïquement ces lignes. Je ne peux tout simplement pas m’empêcher d’apprécier vos efforts titanesques. Bonus pour vous.)

Prime:

Lorsqu'ils écrivent des formules dans une situation de combat alarmante, même les nerds chevronnés ne savent souvent pas où πn, Et où 2πn. Voici une astuce simple pour vous. Dans tout le monde des formules qui valent πn. Sauf pour la seule formule avec arc cosinus. Il est là 2πn. Deux panne. Mot-clé - deux. Dans cette même formule il y a deux signe au début. Plus et moins. Ici et là - deux.

Alors si tu écris deux signe avant l'arc cosinus, c'est plus facile de se rappeler ce qui va se passer à la fin deux panne. Et cela se produit aussi dans l'autre sens. La personne manquera le signe ± , arrive à la fin, écrit correctement deux Pien, et il reprendra ses esprits. Il y a quelque chose à venir deux signe! La personne reviendra au début et corrigera l’erreur ! Comme ça.)